
rand() function returns a random integer in the range of 0 to RAND_MAX. To be more precise I want to use float values instead of integers. I will take the center of the circle as origin point (0,0). Then imagine a 500x500 square and a circle which perfectly fits inside of it. Therefore we can just multiply the ratio by 4 to get an estimate for π.įirst, we need to include math.h library to our program. So if we randomly throw the darts, the ratio should approximate to π / 4. So we can calculate the ratio between the areas of circle and square as following. If we count up the darts that landed within the circle and compare to the total number of darts thrown, the ratio should approximate to the area of the circle divided by the area of the square.įrom the figure, it’s clear that the length of the square L is twice the radius of the circle r. What if we randomly throw darts at a dart board that looks like this. I will use Monte Carlo Method with C programming. There are a couple different ways of estimating π. Lets write a program which approximates the value of π. There are countless number of numerical methods to calculate the value of pi. Since computers can’t work with infinite decimals, they need to approximate pi.

Which means that its value cannot be expressed exactly as a simple fraction. It has infinite digits and it keeps ongoing, forever, without ever repeating. Interestingly, pi is an irrational number, there can be no “final” digit of pi, because it’s an irrational number that never ends. This magical number appears in many formulas in all areas of mathematics and physics. The number π (pi) is a mathematical constant defined as the ratio of a circle’s circumference to its diameter.
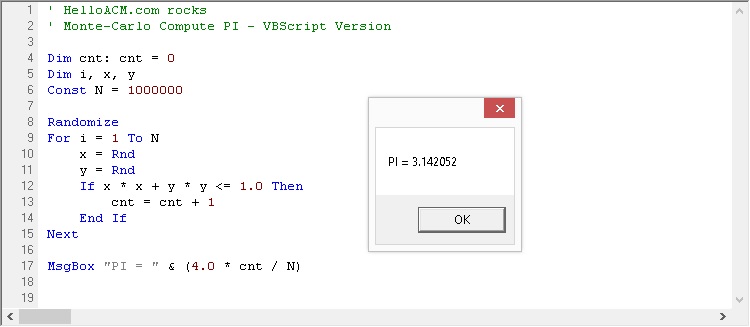
Approximating Pi with Monte Carlo Method | Enes Demirağ Enes Demirağ Approximating Pi with Monte Carlo Method 10 March 2019


 0 kommentar(er)
0 kommentar(er)
